ミラーアレンジメント
| カレイドスコープには二つの基本的なミラーシステムがあります。 ひとつの中心をもつ像を生み出す2ミラーシステムと、 視界全体に反射され広がっていく像を生み出す3ミラーシステムです。どちらも三角の筒状(三角柱)に鏡が組み合わされています。 | |||||||||||||||||||||||||||||||||||
| 2ミラーシステム | |||||||||||||||||||||||||||||||||||
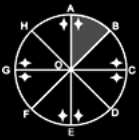
それでは、カレイドスコープの中でどんなことが起こっているのかを示すために、次のような例をとって考えてみましょう。 Oを中心とする円に鏡OAとOBがある。△OABの中にあるオブジェクト(実像)が、鏡OAの反対側、△OHAの相対する 場所に像(虚像)を作る。 | |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
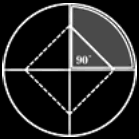
| ミラー角度と映像原理 | |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
| 3ミラーシステム | |||||||||||||||||||||||||||||||||||
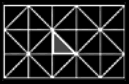
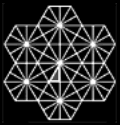
3ミラーシステムは、3枚とも鏡にすることにより、視界全体に持続的に広がる像を作り出します。そして3ミラーシステム では、3つの角度が正確でなければシンメトリーの像にならないので、ひとつの角度だけが問題であった2ミラーよりも、シンメ トリーの像を作るのは難しいといえるでしょう。ここでもまた、鏡の作る角度は円の360度を等分する角度でなければなりません。 そしてシンメトリーになるためのもうひつ重要なルールは、3つの内角の合計が180度とならなければならないことです。 これら二つのルールを摘要するとわずか3通りの組み合わせしか望ましい効果をもたらさないことになるのです。 | |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
| 3ミラーシステムについて更に付け加えるならば上記の説明は、パターンの実像と虚像とが繋がりあって、純粋にシンメトリー のパターンを作るものについてのみ考慮したものであり、一つ二つの角度のみが360度を等分するルールに従った時にも像を作り出すことは可能だということです。しかし、そうやって出来たパターンは見た目にはシンメトリーになっていますがそれは実像の断片的な部分を映し出しているに過ぎない、ということになるのです。 他にも異なったミラーシステムは考えられますが、カレイドスコープのデザインと、様々なイメージのバリエーションを作っていく上で、これらの原理を理解し、基本的な決まりを知ることはきっと役に立つでしょう。 |